小学校低学年の生徒にとって
どうしても越えなくてはいけなく、
そして越えるのがとても難しく、
越えないまま大人になってしまう子も少なくはないハードルがあるので紹介します。
「~~が正しいとすると」 という前提を正しいと仮定して思考する技術です。
これは大人としては「まあわかる」ものですが小学校低学年の生徒には一苦労です。
たとえば、こんな問題です。
==============================
次の文の内容が正しいとすると、そこから確実に言えるのア~エのうちのどれか考えなさい。
「私は海に入ると必ずクラゲにさされる」
ア. クラゲにさされるとき私は海の中にいる
イ. 私がクラゲにさされていないときは私は海にはいない
ウ. 海に入っている私はクラゲにさされている
エ. 私が海にはいらないときはクラゲにさされない
==============================
授業自体は下のように関係図(集合図)を書いてものごとの関係を理解するというものですが、
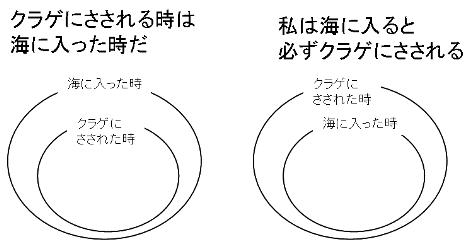
それ以前にそもそも、前提である
「私は海に入ると必ずクラゲにさされる」ということを(とりあえず)正しいと仮定できない生徒がいます。
「え、海に入ってもさされない時があるかもしれないじゃん」
「え、僕は海に入っても絶対さされないから・・・・」
など、前提を前提として据えることができない生徒がいます。
何度説明してもこの壁を越えられない生徒は少なからずいます。
2年生だとクラスの大半の子はこの仮定ができません。4年生だとクラスの大半の子ができます。3年生が分かれ目学年です。この仮定ができるようになると、仮定を土台に思考を、まさに「ロジカルに」すすめられます。難しめの文章の読解がスムーズになり、記述回答のセンスが抜群によくなります。
個々の生徒の成長度合いを判断する時に、この「仮定を仮定として認めて、そして思考を進める」が出来るかどうかを、大きな、とても大事な分岐点として注目しています。
大人が小学生にロジカルシンキングや「思考法」の指導をする際に、
特に注意が必要な部分だと思います。
