私が初めて知ったとき「不思議だなー。」と思ったことです。正多面体とはすべての面が同じ正多角形となっている立体のこと。一番最初に学ぶのは正六面体の「立方体」ですね。直感的にはいくらでもつくれそうなのですが、実は5種類しか存在しません。
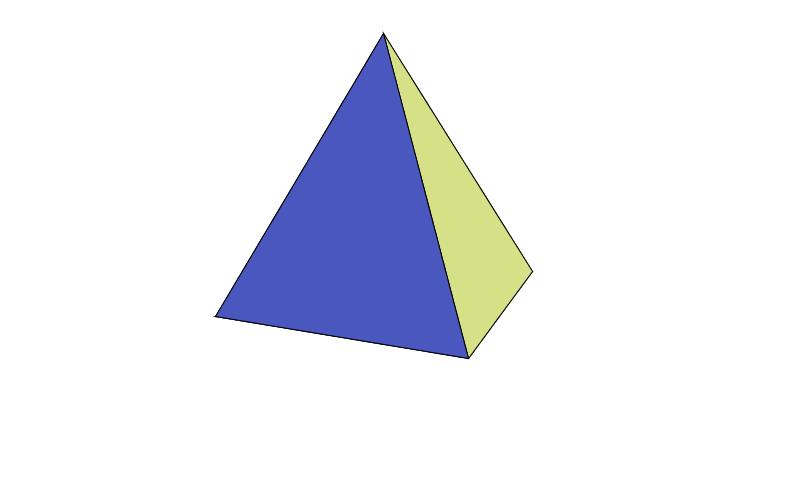
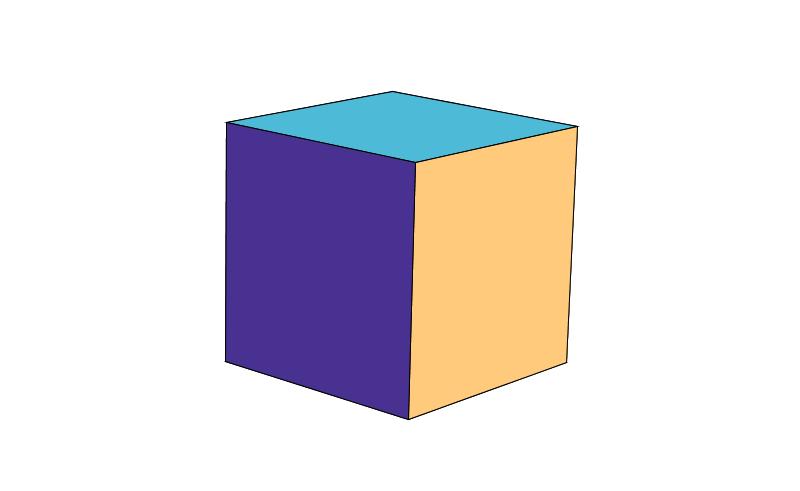
正四面体(面は正三角形) 正六面体(面は正方形)

正八面体(面は正三角形)
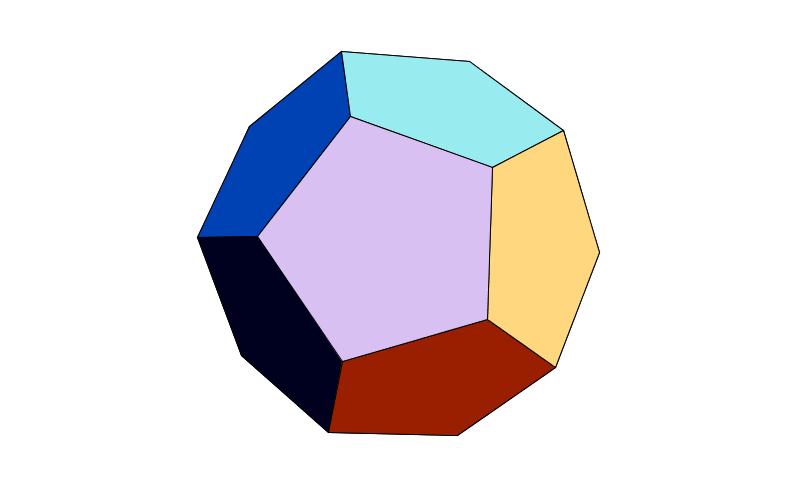
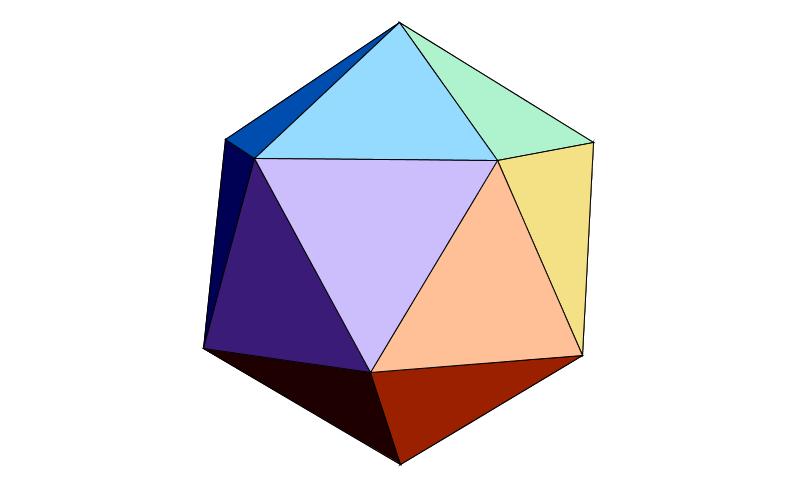
正十二面体(面は正五角形) 正二十面体(面は正三角形)
なぜ正二十面体より面が多い正多面体は作れないのでしょうか。実際に試してみると面をいくらつなげてもお皿のようになってしまうのですが、簡単なものではオイラーの多面体定理
頂点の数 – 辺の数 + 面の数 = 2
から証明できます。紀元前3世紀ごろにエジプトのアレクサンドリアで活躍した数学者エウクレイデス の著作「原論」という本の中でも説明されています。
正多面体は、適切に頂点を選ぶことで別の正多面体を作ることができます。 代表的なものは各面の中心を結ぶという操作で、
正二十面体 ↔ 正十二面体
正六面体 ↔ 正八面体
正四面体 ↔ 正四面体
の様に作ることが出来ます。
