前2回で和が一定の倍数算、差が一定の倍数算をやってきましたが、今週はバラバラ
の倍数算です。
倍数算は、和が一定、差が一定、バラバラの場合の3通りです。特に、このバラバラ
の場合がよく問われるので基本形をしっかりと身についけておくとよいですね。
問題
弟と兄が持っていた金額の比は、5:7でした。弟は、220円、兄は380円もらったの
で2人の持っていた金額の比は2:3になりました。兄がはじめに持っていた金額は
いくらですか。
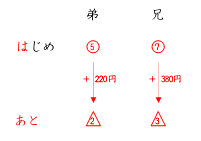
「はじめ」と「あと」で比が変わっているので、まずは表にしてみましょう。
すると以下のようになります。
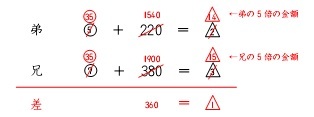
この際、和も差も一定ではないことがわかります。このような場合は下のような表に
置き換えます。また、弟の持っている金額を7倍、兄の持っている金額を5倍するこ
とで○数字をそろえます。差をとると、△数字の1が360円だとわかります。
すると、兄の「あと」の数である△数字の3が360×3=1080円とわかり、
兄のはじめが、1080-380=700円とわかります。
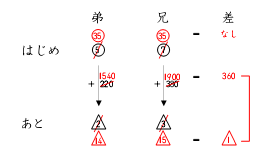
弟を5倍、兄を7倍した数字と取り違えることがあるので、「はあと表」と式にまとめ
た表を分けて書くことがお勧めですが、慣れてくると一連の作業が「はあと表」の中で
まとめられますね。下のようになります。
和が一定、差が一定の倍数算についても、真ん中の表を使うことで解くことができます。
その点においては、式は万能ですね。しかし、やり取りが複数回でてきたり、一定の場
所が何か所か与えられたりする複雑な問題では、式だけでは整理するのが大変です。
そのようなときのために、表にまとめることが大切です。5月に行われるマトリクス算
数では、そういった表にまとめることで視覚化しわかりやすくする問題を多くとりそろ
えているので楽しみにしておいてください。