今週は、先週に引き続き推理の問題を題材に表を使っていきたいと思います。
問題
一郎、次郎、三郎、四郎、五郎の5人がかけっこをしました。5人はそれぞれちがう
色の服を着ています。次のヒントからだれが何位で何色の服だったか答えなさい。た
だし、同じ順位の人はいなかったものとします。
ヒント
①三郎は最下位ではなく黒の服も青の服も着ていません。
②赤の服を着た人は次郎の次にゴールし、赤の服の人の次にゴールしたのは五郎でした。
③青の服か白の服を着ている子が四郎です。
④一郎の前にゴールしたのは緑の服の人で、その前にゴールしたのは四郎でした。
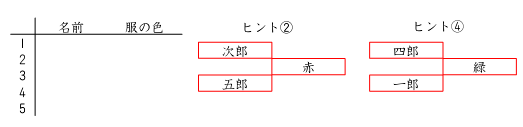
順位、名前、色を表にしてきます。このとき、表の中に入るのはそれぞれの名前と服の
色になります。そして、ヒント②、④をパズルにして埋め込んでいきます。
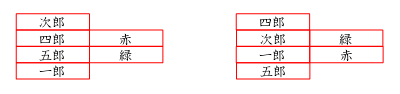
ヒント②と④のパズルを合わせる方法は、次郎と五郎に間に、四郎が入るか、一郎が入
るかの2通りしかありません。(それ以外の合わせ方では6人になってしまう。)
このとき、左側の図ではヒント③に矛盾がおきます。よって、右側の図が正しい合わせ
方ときまります。すると、ヒント①より三郎は最下位ではないので1位にきまります。
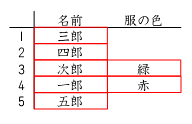
ここまでくれば、条件に合った服を入れるだけですね。残った服の色は、白、青、黒。
三郎は、黒でも青でもないので白にきまります。残る服の色は黒と青。すると、ヒン
ト③より四郎が青にきまり、最後に残った黒が五郎となりますね。
このように、複雑な推理であっても表にし、パズルを使うことで前後、左右の関係が
わかりやすくなります。ただ、この表にたどり着けるかがポイントではありますが。
先週扱った問題のように、まずはどのような表で攻めようかと考えることが大切にな
りますね。