ロジム公開講座実施のおしらせ

表で解く！　マトリクス算数

第４回　表で解く底面積比と高さと体積比 (9/23実施) から続く、
第５回講座のご案内です。

	小学校６年生（比を既習の5年生も受け付けます。過去回が未受講の方もお申込み可能です）「ロジスペ！」はロジム生以外も受講可能な公開講座です。
	メール info2@lojim.jp　もしくは　電話 03-5646-5646 受講希望の旨をご連絡下さい。
	3,150 円

場所：ロジム代々木教室

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
【第５回】表で解く速さの平均・流水算・歩幅・エスカレーター問題 10/14(月祝) 14:00～16:00
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
子どもたちの多くは速さの問題と聞くと、旅人算を利用した問題を考えます。しかし、その典型的な問題から外れた速さの問題に対しての処理は経験も少なく失点しがちになります。
この講座では、そのような速さの問題にスポットライトをあて学習していきます。

問題例　(流水算)
『ある流れのある川のＡ地点からＢ地点を往復するボートがあります。Ａ地点からＢ地点は12km離れていて、上りにかかる時間は１時間でした。ボートの静水時の速さが時速15kmのとき、下りにかかる時間は何分ですか。』

速さについての情報がいくつかでてくるので、それを取り違えることで多くのミスが生まれます。
取り違えをなくすために、表にまとめてみると以下のようになります。

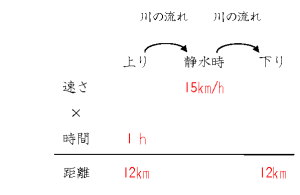
表の『上り』が距離と速さがわかったので、上りの速さを求めることができます。
上りの速さは、12÷1＝時速12kmとなります。このときの、上りの速さと静水時の速さの違いは、
川の流れの影響によるものなので川の流れの速さは15－12＝時速３kmとなります。

表より、下りの速さが求められます。下りの速さは、15＋３＝時速18kmとなります。
よって、下りにかかった時間は、12÷18＝2/3時間＝40分となります。