3年生
論理的思考の土台を完成させ、
高学年の中学受験レベルの学習へのしっかりした足場を築く

4年生から本格化する、より高レベルの学習に対応していくために、論理的思考の土台を完成させます。
あらゆる未知の問題に思考と手をとめずに、考えていく姿勢を身につけます。
本科ロジカルキッズワーク

全国の書店で大人気のロジカルキッズワークのクラスが登場!
ロジムの手法が詰まったロジカルキッズワーク新装丁で発売中!
(2024年現在累計14刷)
特徴
- 週1回 110分の少人数制集団授業
- 算数、国語、ロジカルシンキングの総合学習
- 宿題は個人の能力に応じた細かい添削指導
- 定着度を計る「到達度確認テスト」を毎月実施
- 《無料特典》通信講座「まいにちロジム(Kコース)」付き
ロジカルキッズワークとは?
発表とディスカッション重視の授業!
数(算数)、ことば(国語)、ロジカルシンキングの要素を盛り込んだ総合学習講座です。
ロジムオリジナル教材を用いて論理思考を養うレクチャーメソッドと、迅速な試行錯誤を鍛えイメージ思考を養うゲームメソッドの2つの形態から成り立ちます。
算数や国語といった科目間の垣根をなくし、「考え方・頭の働かせ方」ごとに集中的に取り組み、学習効率を最大化させます。

論理的思考力を育む2つのメソッド

正しく考える練習をする授業/思考の長距離走トレーニング
「よく考えなさい」と言っても、「考える方法」が分からないからこそ、前に進めずにいる子どもたちが多くいます。
・前提を組み合わせる方法
・仮説を組み立てて解決に向かう方法
・効率的に記憶するために情報を整理する方法
など、多くの物事には「正しく考える」方法があります。
レクチャー授業では、「課題を整理する」「問題を解く」思考方法を伝え、じっくり一つの問題に取り組む能力を鍛えます。
速く運用する練習をする授業/思考の短距離走トレーニング
「そもそも何を問われているのか」
を素早く的確に理解し、選択肢を整理し、知識を運用する力をゲーム形式で楽しく鍛える授業です。
「速く運用する」能力は、漫然と問題演習を繰り返していたのでは身につきません。
ゲーム形式の授業では、時間制約の中で読む・聞く・算術処理などをすることを通して、数多くのトライアンドエラーを経験することで、
自然と瞬時の判断力が身につくように設計しています。
個人の能力や個性に応じた細かい宿題添削指導
毎授業時に「てんさくプリント」という宿題冊子が配布されます。各授業ごとに設定された締め切り日までに提出していただき、添削を行い返却します。解答の状況に応じて、ヒントを伴ったやり直しが指示され数回の往復添削が行われます。
従来のロジムのカリキュラムである、1つの空間、1つの集団での知識共有・切磋琢磨という講義スタイルの授業と、生徒個人の能力や個性に応じた細かい指導を可能とする通信添削を融合させました。
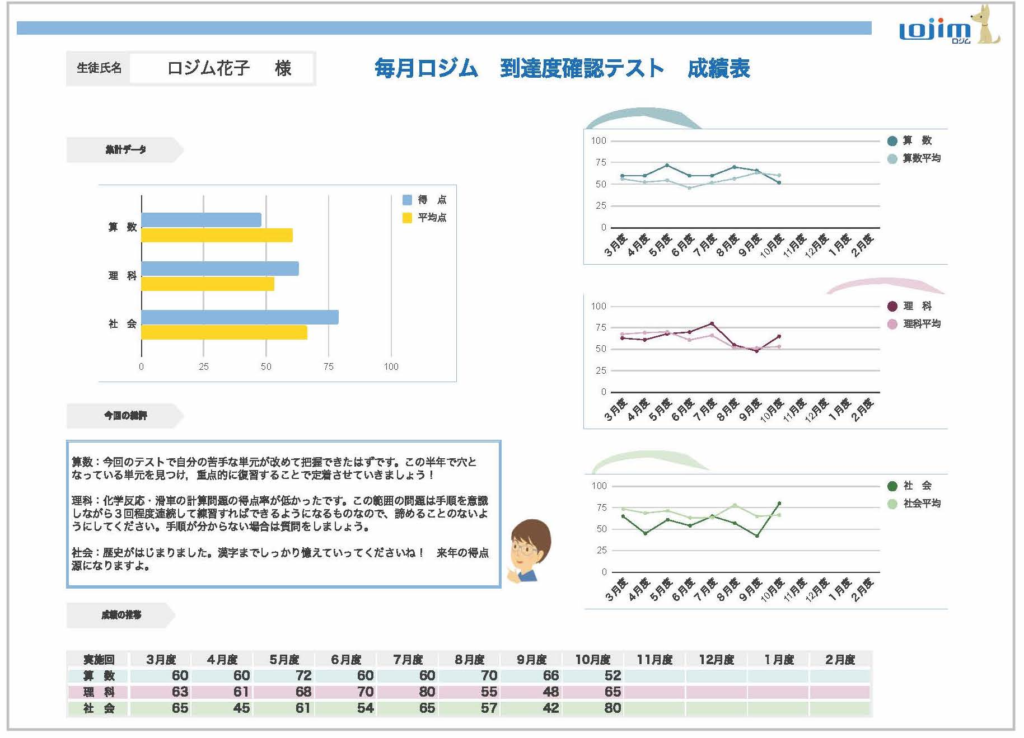
《月1回実施》到達度確認テスト
本科ロジカルキッズワーククラスで扱った内容の定着度を計るテストを毎月行います。 1ヶ月間の学習範囲を翌月1日~10日の間にテストを行います。
習熟度を一覧表にし、学習計画の指針として活用します。
《無料特典》「まいにちロジムKコース」
本科ロジカルキッズワーククラスの受講者は、ロジムの通信教材「まいにちロジム」の基礎的な計算練習用コース(Kコース)を無料で受講できます。
平日10分の日々の宿題として学習習慣をつけること、思考の道具としての計算力を確固たるものにすることを目的としています。


【単科】算数基礎マスター
特徴
- 週1回 80分の少人数制集団授業
- 計算力を中心とする算数の基礎力アップ講座
- 個々の進度状況に合わせた指導を実現
算数基礎マスターとは?
個々のペースに合わせて算数の基本技術を習得する講座
ロジカルキッズワーククラスでは扱わない、算数で身につけておくべき基本技術を演習形式で学習します。
思考力を養成するロジカルキッズワーククラスでの学習効果を最大限にするため、4年以降の学習の中心となってくる、より高度な算数の学習にスムーズに入っていくための基礎力を身につけましょう。

- ロジカルキッズワーク内の算数との違いは?
- 算数基礎マスタークラスは、算数の基本技術の習得と、論理的な思考をするために必須の計算や土台となる定義などを素早く正確に運用できる力を養う講座です。
四則演算や図形の定義、性質・線分図の利用の仕方、単位の変換と計算など、ロジカルキッズワーククラスでの学習や、4年以降の算数の学習で必須となる基本技術を習得します。
- どんな力が身につくの?
- 個々の進度に応じて演習を行い、講師のアドバイスをもとに必要なところを効率よく反復練習したり、より難易度の高い問題に取り組んだりしながら、確実に素早く算数の基本技術を運用できる力を身につけます。
これにより、計算などに思考を邪魔されることなく、問題の本質を考え、スムーズに試行錯誤をできるようになり、応用力が高まります。
- 宿題はあるの?
- 個々の授業内での進捗に応じて、授業で扱った問題の解きなおし、類題などが宿題として課される場合があります。
- どんな子が対象?
- 個々の進度に応じて課題に取り組むため、算数が苦手な子も得意な子も、確実に力を伸ばすことができます!ロジカルキッズワーククラスとの併用をオススメしております。

![学習塾ロジム [代々木・門前仲町・江戸川橋の学習塾]](https://lojim.jp/cms/wp-content/uploads/2024/04/ac95a853b9199672b0e023ac70f070f3.png)

