先週は差が一定の倍数算をやりましたが今週は和が一定の倍数算です。
こんな問題でも倍数算が利用できるという問題を1つ。
問題
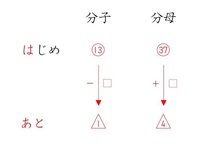
37分の13という分数があります。この分数の分母に□をたし、分子から□ひくと、
4分の1になります。□はいくつになりますか。ただし、□に入る数は同じものとします。
今回のポイントは、分数が分子と分母の比にできるということです。
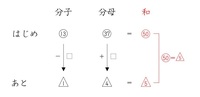
すると、「はじめ」と「あと」で比が変わっているので、「はじめ」と「あと」の表(はあと表)でまとめることができます。
分子と分母のやりとりとなっているので和は変わりません。ここに着目し、比の和をとると○数字は50、△数字は5となります。これが等しいので、比を50でそろえます。
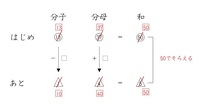
比を50でそろえることで、○数字と△数字が同じ比で表すことができました。
この表より、分子から少なくなった数が□数字の3、分母から多くなった数が
□数字の3とわかります。よって、□に入る数は3となります。
今回の問題については、分数も比として扱えるということに着目した問題ですね。
そう考えると、「はじめ」と「あと」で比が変わる問題はたくさんあります。
数が変化する問題は、「はあと」の表にまとめられないか疑ってみてもよいかも
しれませんね。