今回は、先日『ロジスぺ!表で解くニュートン算』扱われたニュートン算を表にします。
問題
ある劇場では、入場時刻にすでに長い行列ができていて、入場開始後も1分あたり20人
の割合で行列に加わる人がいます。入場窓口4つにすると、行列は45分でなくなります。
また、入場窓口を5つにすると、行列は27分でなくなります。入場開始時刻には何人の
行列ができていましたか。
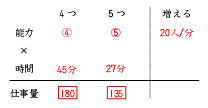
前回の仕事算の表に、増える欄を加えます。そして、わかる数値をいれたら、計算でき
る場所に数字を入れていきます。今回は、窓口4つのときと、窓口5つのときの仕事量
(それぞれの窓口が入れた人数)が計算できます。
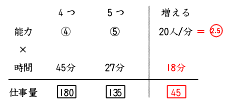
はじめに並んでいた人数が同じなのに、仕事量(それぞれの窓口が入れた人数)が違うの
は、時間がかかった分多くの人が並んだせいです。よって、時間の差によって、仕事量
の差がうまれたことになります。時間の差の18分により、仕事量が45増えたとわかりま
す。よって、増える能力は、45÷18=○数字の2.5となるので、①の能力は
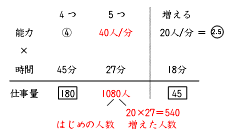
20人/分÷2.5=8人/分とわかります。⑤の能力は、8人/分×5=40人/分となります。
窓口5つの仕事量は、40×27=1080人となります。このうち、増えた人数は20×27=540人
です。よって、はじめにいた人数は、1080-540=540人とわかります。
はじめにいた人数は、(40-20)×27=540でも求められます。
ニュートン算は、仕事算とくらべて、一定量増える数がはいるので作業が複雑になりま
す。大事なことは、今扱える数は何なのかをはっきりさせ、それを利用することです。
今扱える数をはっきりさせるうえで表の存在は役に立ちます。