今週は、追いこしの旅人算を表にして考えていきます。この考え方も実は差集め算
なんですが、表にして比で考えていきます。
問題
弟は分速60mの速さで学校に向かいました。兄は弟が出発した4分後に分速100mの
速さで弟を追いかけました。兄が弟に追いついたのは家から何m地点ですか。
追いこしの旅人算で解くと、「兄が出発したときの、2人の距離の差は、60×4=240m
。この差を1分あたり、100-60=40mずつ縮めるので、この差が縮まるまでにかかる時
間は、240÷40=6分となる。兄が4分歩いた位置なので、100×6=600mとなる。」
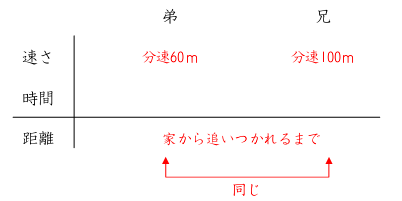
このようになります。これを、表にすると下のようになります。
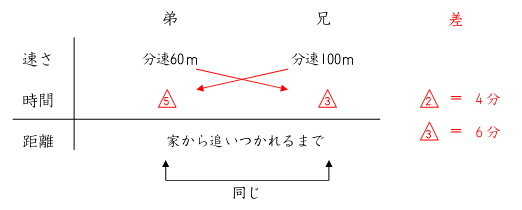
2人の歩いた距離(家から2人が同じ場所にくるまで)が同じなので、時間が逆比に
なります。
ここで、時間の差が、△数字の2とわかります。この差は、それぞれの速さで家から
追いついた場所まで行ったときにかかる時間の違いになるので、△数字2=4分(弟が
長く歩いた分)となります。△数字の3が、4÷2×3=6分(兄が歩いた時間)とな
るので、家から追いつくまでの距離は、100×6=600mとなります。
速さの『差集め算』、『旅人算の追いこし』ともに、同じ表を扱うことで求めることが
できます。ポイントは距離が一定ということです。